波动市中的风险平价策略及启示
本文介绍了大类资产配置中的风险平价策略。由于股票资产的波动性远超其他资产,传统投资组合不成比例地暴露在股票市场的非理性波动之下,为降低投资组合整体波动,风险平价策略用固定收益产品大量取代股票资产,并引入杠杆放大收益。风险平价策略将风险与“再平衡”作为核心,定位于提升组合的长期回报,而非追逐“卓越收益”。
一
波动性的危害
(一)波动性伴随更低的累计收益率
投资者普遍地混淆复合收益率与算数平均收益率。进行收益-风险权衡时,投资者脑海中的“固有印象”往往是一张概率分布图:对于典型的横截面收益,高波动(高风险)意味着投资虽然承受巨大的尾部风险(收益率落在左边尾部),但同时意味着获得极高收益的机会更大(收益率落在右边尾部),这种理念“诱惑”投资者为实现成倍的收益主动追逐波动性。
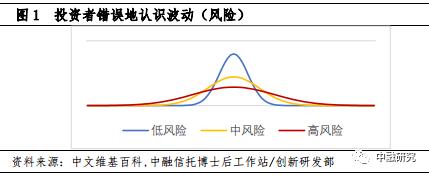
即使最朴素的投资经验也警示,高波动会拉低投资收益。如果投资者在某类资产第一年获得100%的回报,第二年收益率为-50%,那么该资产两年中的算数平均收益为25%,但复合收益率为0%。复合收入率与算数平均收益率之间的差异,最直观的近似为:
G=A-V/2
其中,G为复合(几何)收益率,A为算数平均收益率,V为方差[1]。波动性越高,复合收益率越低,最终积累的财富就越少。并且在最坏情形下,如果波动性在12%的上下3个标准差浮动,初始财富可能损失超过一半。
(二)波动来自哪里股票收益率的波动性远高于固定收益,常见的60/40配置策略中,组合90%的风险源于股票的波动。股票市场总是过度波动,超过了由股息变动决定的趋势。席勒(2015)指出,媒体宣称的因为企业的短期前景而引起股市波动的说法具有误导性,因为历史上的衰退一直以来都是短暂、微弱的,暂时性的经济萧条实际上不会对股价产生实质影响。研究表明,只有15%的美国月度回报率的波动是由于有关未来股息的真实信息引起的。事实上,历史中一些主要市场的价格变动是由人们的想象和社会心理因素推动的。各种社会角色在泡沫的产生、膨胀和破裂中起到不同程度推动作用:
1.新闻媒体热衷于介绍具有较强故事性的内容吸引客户和读者,新闻媒体对人们过于情绪化的非理性投资行为产生了很大的影响。
2.公众人物如果总是发表股票市场回报率在今后几年里降低或存在泡沫等言论,会使他们面临陷入困境的风险,更倾向于保持沉默。
3.市场分析师与投资银行、经纪人、企业共同分享收益。
4.在缺乏“导航”的迷雾中,投资人只能依赖股价变动本身来验证自己的想法。在泡沫产生的过程中,随着价格不断上涨,人们的想法不断地改变,那些原认为存在泡沫的人,会产生自我怀疑并开始思考是否是真的基本面的经济因素推动了价格上涨。价格上涨持续的时间会强化人们的这种信念;反之,如果价格长时间没有上涨,人们会逐渐产生不满情绪,即使实际经济指标有所增长,投资者的不满情绪也可能导致市场反应迟滞甚至价格下跌。
股票市场的繁荣和萧条由大量投资者各自无关紧要的观点共同作用,市场总是处在无端的过度波动之中。
二
平衡收益与波动
(一)最优投资组合
由于波动性过高,单独来看,多数权益资产长期中提供的投资回报并不具有吸引力,而现代投资组合理论的发展使得投资者可以跳出单一资产约束,将不同的股票、债券、另类资产打包成一个资产组合,得到希望的收益率并承担相应波动。
投资者往往忽视“再平衡”对于投资组合的意义。如果投资者只是简单地进行分散投资而任由组合中各类资产占比随着市场波动变化,那么投资组合仅仅对投资者形成心理安慰,投资者实际上分别持有各种高波动的资产,任由波动在长期中不断拉低复合收益率。
有效边界描述了不使用杠杆的情况下,市场中各类资产组合所能获得的预期收益-风险组合。对于低于有效边界的组合,总能找到更好的替代资产,使得投资者承担更小的波动,或取得更好的预期收益,“无杠杆最优投资组合”代表在该组合下,收益-风险之比达到最高。
在不使用杠杆时,投资者要获得6%的期望收益只能选择右侧的“均值-方差”组合;使用杠杆后,投资者可以额外调用一倍杠杆买入“无杠杆最优投资组合”,最终落在“100%杠杆最优投资组合”位置,此时,投资者的预期回报率(算数平均收益)为6%,但波动率不足原来的一半。
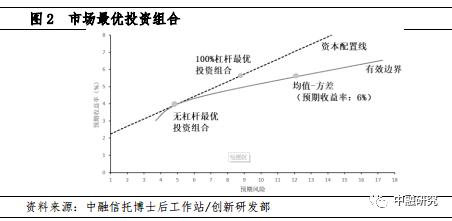
(二)实践最优投资组合困难重重
均值-方差模型的一个重要优势是,优化问题的输入参数(波动率、相关系数和预期超额收益率)可以用历史数据代表,模型的执行相对简单。但均值-方差模型存在局限:
首先,投资组合的权重对于资产的预期超额收益假设的改变十分敏感,而对资产的超额收益率的估计基本依赖主观判断。
其次,相关性会随时间而改变,资产之间的相关系数通常在熊市期间大幅上升。从下跌风险角度看,当投资组合的损失分布有肥尾时,在既定收益率期望下最小化方差投资组合不一定是最优的。
总的来说,波动率的估计误差一般远远小于相关性和超额收益率的估计误差。战略性资产配置的一个实用办法是在有效边界上寻找唯一的波动率最小的投资组合。
三
风险平价策略
(一)构建风险平价策略组合
1.风险平价中的资产比例
如何确定风险平价组合的构成,业界并没有标准的答案,易于实践的两种方法包括:
(1)忽略大类资产配置之间的相关性,利用资产波动的倒数配置大类资产,使得每一大类资产对整个投资组合贡献的波动率都相同。
(2)根据标准差和相关性来确定每个资产类别对总体投资组合风险的边际贡献,解出一个组合,组合中每个大类资产对总投资组合风险的边际贡献是相等的。
2.测度波动性
资产收益率的波动率,可以从过去1到2年的每周历史数据或者已交易期权的价格中推导出来。对于投资期限长达多年的战略资产配置决策来说,用5到10年的月度数据更为合适。
3.杠杆
由于配置了大量低收益固收资产,组合通过加杠杆来获得令投资者满意的收益。风险平价可以利用债券的分散化力量将其变成经济衰退下更为有效的风险分散工具,同时可以配置更多的高风险、高收益证券类资产,例如私募股权和对冲基金。
4.再平衡
如果没有再平衡操作,构建投资组合的意义也将大打折扣。
(二)风险平价策略的资产构成
风险平价策略包含大量固定收益证券,大宗商品配置比例也更高。作为对比,传统投资组合以高预期收益的股票资产为主,美国股票和非美国股票占据投资组合的绝大部分头寸。
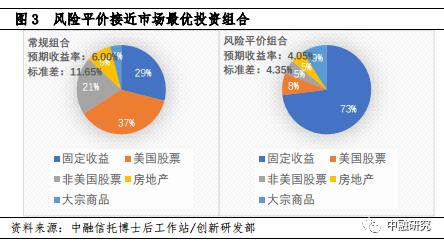
(三)风险平价策略的优势
Asness等(2012)认为,风险平价足够接近最优投资组合,主要因为两类组合都超配了低收益的固定收益资产。他们认为市场中普遍存在杠杆厌恶,政策或心理约束推动投资者远离杠杆,相比更安全的资产,投资者更倾向于选择高风险资产,形成市场低效率。一个杠杆成本足够低、主要由相对安全资产组成的加杠杆组合,可以利用这种低效产生更高经风险调整的收益率。分析1986-2010年间全球10个发达国家的市场的结果表明,在每种情况下,风险平价策略都比传统的60/40投资组合有更高的经风险调整的收益率。
(四)风险平价策略的潜在风险
1.风险平价可能长期落后传统策略
2009年全球金融危机后,圣迭戈郡雇员退休协会将整个投资组合的管理外包给Integrity Capital,后者在总投资组合中实施风险平价策略,这一尝试在2015年7月被放弃,因为在金融危机后的7年牛市中,投资组合的表现一直落后于同行。
2.债券与股票之间的关联性不稳定
1996~2016年市场对风险平价策略十分有利,这一时期股票和债券一直呈负相关,享受较高收益率的同时,整个投资组合的波动率也很低。情况并不总是这样,在加了杠杆的情况下,假设的负相关实际是正相关的,那会对投资组合非常不利(在极端的“滞胀”环境中,股债收益率呈现正相关,这种情形在2021年下半年出现)。
3.杠杆
发达金融市场中,机构投资者获得杠杆的来源变多,从简单的信贷额度到期货和期权市场,到收益互换,到债务抵押债券(CDO)和其他带有内在杠杆的各种工具,使得最优的杠杆资源变得更加复杂。
首先,在一定的目标收益率下,借款利率即使发生相对小幅的变化,仍然可能影响风险平价组合的杠杆率。
其次,资产端发生的变化也会影响所需杠杆率。譬如,经济危机后,量化宽松和其他宏观因素使风险资产的预期溢价降至非常低的水平,低收益率加上规模处在历史高位的政府债券使得债券市场的预期波动性降低至历史低点,在风险平价框架内,债券波动性的下降会带来更多的债券配置。债券在投资组合中的高份额与风险资产的低收益率相结合,将导致无杠杆风险平价组合的预期收益率达到历史最低水平,实现目标收益率所需的杠杆率就越高。
最后,在市场混乱,流动性溢价高企的时期,交易对手对高杠杆率的投资组合会要求更高溢价,或者可能会完全收回自己的信用额度,对风险平价形成破坏性影响。
四
风险平价的实践
最著名的应用来自桥水基金1996年推出的“全天候”投资组合。“全天候策略”通过平衡经济增长和通胀风险的方式来进行风险配置,并将其设计成为在所有经济环境中都表现良好。成立至今年化收益率接近10%。与风险平价类似,更高波动性的资产占比更低。
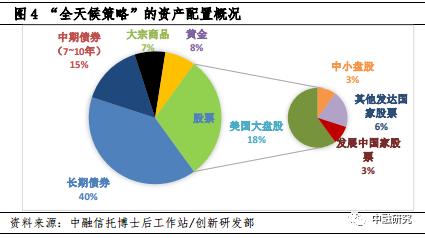
五
总结
波动性使得资产的复合收益率显著低于算数平均收益(横截面收益率或预期收益率),拉低投资者的长期回报。最优投资组合提供了最佳的收益-波动权衡,但在实践中,收益率和相关性难以捉摸的特征使得理论上的最优投资组合难以落地。风险平价策略使用固定收益产品取代高波动的股票资产,并使用杠杆放大收益,和理论中的最优投资组合十分接近,其风险主要来自:在股票牛市跑输传统组合、股债相关性转正以及高杠杆。
注[1]:这个简单的近似公式适用于10%左右的收益率和20%以下的标准差,更大数值下的估算参见Mindlin(2011)。
参考资料:
Asness, Clifford S., Andrea Frazzini and Lasse H. Pedersen. Leverage Aversion and Risk Parity. Financial Analysts Journal, vol. 68, no. 1, 2012: 47-59.
Dimitry Mindlin, “On the Relationship Between Arithmetic and Geometric Returns,” CDI Advisors LLC, August 2011.
曹实. 多资产投资策略:资产管理的未来,北京:北京大学出版社,2020.
希尔达·奥乔亚-布莱姆伯格. 投资的原则,北京:中信出版社,2022.
罗伯特·J. 席勒. 非理性繁荣,北京:中国人民大学出版社,2016.
注:以上内容不作为任何投资或建议,仅供参考。
交易商排行
更多- 监管中EXNESS10-15年 | 英国监管 | 塞浦路斯监管 | 南非监管92.42
- 监管中FXTM 富拓10-15年 |塞浦路斯监管 | 英国监管 | 毛里求斯监管88.26
- 监管中axi15-20年 | 澳大利亚监管 | 英国监管 | 新西兰监管81.40
- 监管中GoldenGroup高地集团澳大利亚| 5-10年85.87
- 监管中Moneta Markets亿汇澳大利亚| 2-5年| 零售外汇牌照79.67
- 监管中GTCFX10-15年 | 阿联酋监管 | 毛里求斯监管 | 瓦努阿图监管60.85
- 监管中VSTAR塞浦路斯监管| 直通牌照(STP)80.00
- 监管中IC Markets10-15年 | 澳大利亚监管 | 塞浦路斯监管91.81
- 监管中markets4you毛里求斯监管| 零售外汇牌照| 主标MT4| 全球展业|75.06
- 监管中CPT Markets Limited5-10年 | 英国监管 | 伯利兹监管92.51


