深度探索FHE：机制、用例、问题及项目lg...

作者：Taiko Labs；翻译：金色财经xiaozou

我们将在本文简要解释FHE是什么及其运作机制，探索其在区块链之内及之外的用例，并探讨相关问题和限制条件。最后，我们再来看一些区块链FHE项目。

1、FHE简介

· FHE的全称是Fully Homomorphic Encryption，即全同态加密。

· FHE最初于20世纪70年代提出。然而，直到2009年，全同态加密领域还没有取得太大进展。最好的技术可以支持无限次的加法运算，但只支持一次乘法运算（而理想的结果是无限次的加法和乘法运算）。

· Craig Gentry在2009年做出了开创性的飞跃，展示了支持无限次的加法和乘法运算的第一个FHE结构。

· FHE支持加密数据处理。

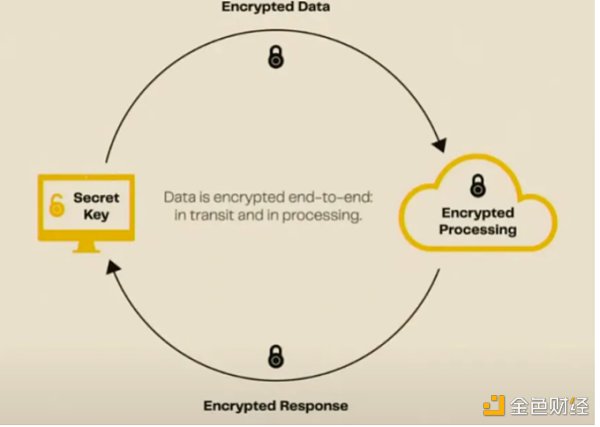
· 也就是说，它对加密数据进行运算。

· “Fully”意为既包含加法又包含乘法。加法同态：E(m₁) + E(m₂) = E(m₁ + m₂)；乘法同态：E(m₁) * E(m₂) = E(m₁ * m₂)

· 从数学角度来看，FHE是一个已解问题。从工程角度来看，这项工作正在进行中，其核心瓶颈是性能。

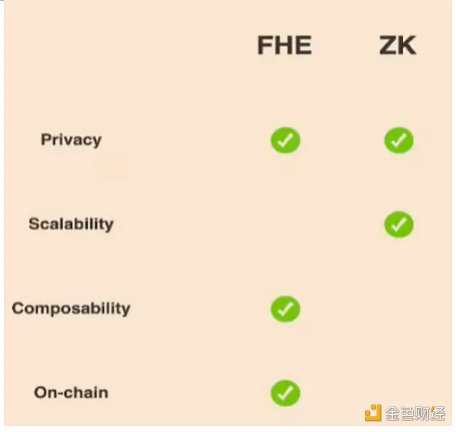
· FHE并不被视为是一个自给自足的解决方案（至少目前还不是），而是提供隐私保护的一个组件，有望与ZKP、MPC和TEE协同工作。例如，虽然FHE在计算过程中保护了数据隐私，但并不保证计算的可靠性。为了缓解这一问题，FHE可以与ZKP相结合，以实现保密性和计算可靠性。另外，还可以将FHE和MPC相结合来提高效率。使用FHE对加密数据进行线性计算，用MPC处理非线性计算。

2、FHE运作机制

· 密文=加密数据+噪声，也就是在加密后的数据中加入随机噪声以保证安全性。

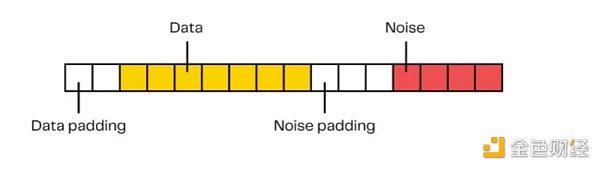
· 然而，现在所有的计算不仅仅是对数据进行计算，而且是对添加了噪音的数据进行计算。

· 另外，经过几次运算后，噪声开始增长并溢出到实际数据位，这可能导致计算结果错误。具体的增长速度取决于使用的是哪种编码。例如，可以是在最低有效位（LSB）添加噪声，在最高有效位（MSB）添加消息，或者也可以是相反的操作，还可以包含padding填充（添加零位）：

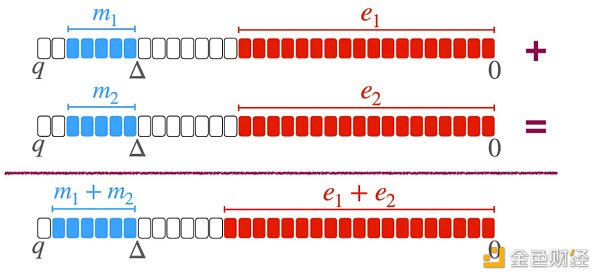
或者将消息和错误编码在一起：

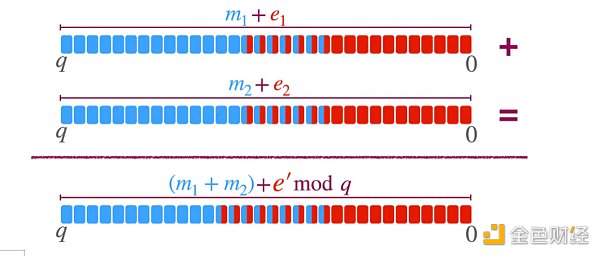
· 为了应对噪声增长，我们可以准备足够的空间。然后，它会变得相当高效快速，但可用运算的值无论如何都是有限的（无论噪声空间有多大）。对于智能合约来说，这是没用的，因为智能合约有时是无限可更新的（例如，ERC-20）。

· 另一个问题是，通过为噪声添加空间，只能进行加法和乘法运算，而比较和非线性函数则常使用多项式逼近。它在机器学习案例中运行得很好，但对于智能合约来说，情况可能并非如此（例如，用户没有足够的资金，但交易却通过了——这并不是件好事）。

· 为了减少噪声，也可以使用bootstrapping同态刷新。Bootstrapping是一种特殊操作，它将噪声重置到其正常水平。它支持永久计算，但这种操作又慢又贵（就内存消耗和计算成本而）。这也就是为什么很多时候，当我们在谈论FHE研究时，我们实际上在谈论的是bootstrapping加速。

· 另一种解决方案是TFHE——这是一种支持无限次计算和任意精确值（而不是近似值）的可以快速bootstrapping的方案。TFHE使用bootstrapping操作来计算同态查找表（lookup table）。任何函数都可以编码为一个lookup table。所以，TFHE消除了近似值和操作次数的限制。

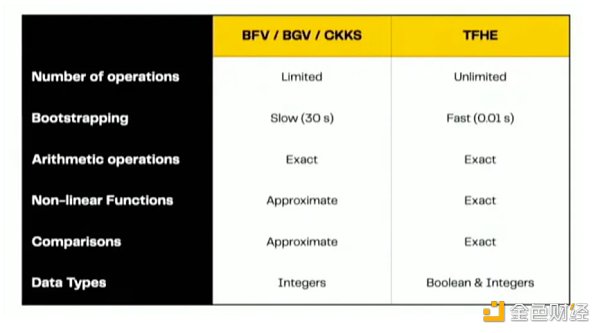
· 还有一个值得关注的FHE方案就是CKKS（近似值计算同态加密）。其性能有望逼近TFHE，但有着不同的优点。CKKS可以在进行不同操作，如bootstrap、多数据流同时操作（SIMD，单指令/多数据流），并使用更大的整数和浮点数bit表示。CKKS支持加密消息的近似加法和乘法运算，以及用于管理明文大小的可选重缩放过程（rescaling procedure）。此过程将密文截断为较小的模数（modulus），从而生成明文近似值。主要想法是在包含主要信息的有效数值后面添加噪声。为了安全起见，这种噪声最初被添加到明文中，但被视为在近似值计算过程中发生的错误，通过重缩放过程可以与明文一起被减少。因此，解密结构输出的是具有预定精度的明文的近似值。计算过程中的精度损失受电路深度的限制，与未加密的近似值计算（如浮点运算）相比，精度损失最大可超1 bit。由于重缩放过程，密文模数的bit大小随被计算电路的深度呈线性增长。CKKS还可以应用于有效计算倒数、指数函数、逻辑函数和离散傅里叶变换等超越函数。

3、FHE用例

（1）常规用例

· 私密链上计算：

加密交易数据：对交易中包含的数据进行加密。

加密状态更新：状态更新时保持加密状态。

加密链上数据：存储在链上的数据保持加密状态。

私密智能合约：私密计算+私密数据。私密智能合约中的整数是加密整数。不应对常规的智能合约编写逻辑进行其他更改。最棘手的问题是，如果余额被加密，智能合约该如何查看余额。

· EVM中的FHE（以Zama fhEVM为例）

fhEVM并非区块链，而是其他区块链可以使用的加密组件。它还包括针对FHE优化的阈值协议，是用于表达基于加密数据运行的智能合约的solidity库和用于构建dapp以正确加密数据并与加密区块链交互的dapp SDK。

fhEVM背后的机制：

所有数据都在一个全局FHE公钥下加密。

全局秘钥是使用阈值协议生成的（秘钥的各部分在验证者之间分布）。

输入数据使用FHE公钥加密。

对加密数据的计算由验证者本地完成。

验证者可以使用阈值协议对数值进行解密。

也可以使用阈值协议在另一个公钥（我们称其为“公钥a”）下对数值进行再加密（不需要解密）。再加密后的值可以由公钥所有者解密。

（2）具体用例

· 链上盲拍

链上盲拍两个阶段：叫价阶段和申领阶段。叫价阶段由用户对加密数量的代币（使用加密的ERC20合约）喊价。当拍卖结束后，合约同态确定最高出价人。最后，合约只公开中标人，而对中标值和非中标值保密。

· 买卖指令在执行之前不为公众所知的市场。

· 机密的ERC-20代币。

· 加密健值（key-value）数据库。

· 无需信任的桥：使用加密密钥同态签名桥交易。

· 保密投票：选择及代币金额是加密的。

4、FHE问题

就 FHE区块链而言，整个网络只有一个密钥。谁持有解密密钥？这个“谁”将定义安全级别。正如Secret Network所建议的那样，密钥片段被分发到每个oracle节点——也就是说，用到了阈值MPC。关于MPC安全的问题有很多，对依赖MPC安全的FHE安全的质疑也有很多。

改进安全性假设的一种方法是在FHE内部部分运行解密。但是，如果出于安全考虑FHE是可选的，那么使用它还有另一个原因：擦除问题。当Oracle节点应该被轮换时，应该保证前一个节点已经删除了曾持有的密钥片段。

然而，与MPC相比，FHE表现更优，因为它将大部分计算外包给完全无需信任的节点，只有一个半受信quorum来进行阈值解密，与MPC不同，MPC下由quorum完成所有工作。它的工作原理如下：密钥片段被生成并在验证者之间共享；每个验证者执行部分解密；部分解密被聚合产生完整的解密值。其安全性依赖2/3诚实验证者假设。但是，验证者集应该是固定受限的。

就Secret Network而言，网络验证者需要在共识时间内做出断言。他们应该如何访问解密数据？当然不能使用oracle，因为会破坏隐私。解决之道是两轮共识机制。第一轮是对应该解密的内容达成共识。也就是说，oracle等待大多数验证者发送相同的解密请求，然后再进行内容解密。随后，验证者更新链状态并将区块添加到区块链上。

如何防止用户解密其他用户的数据？如果用户只编写一个用来解密输入数据的合约，并提供其他人的加密数据作为该合约的输入数据，会怎样？解决方案是零知识证明！用户应该提供他们发送到网络的每个加密输入的ZKP，以证明用户确实知道他们以加密方式发送的数据值。

FHE的关键技术问题就是速度慢，比已知的替代方案要慢很多。

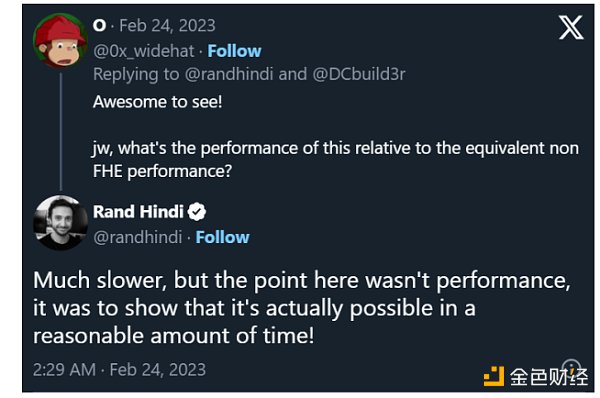
慢多少？

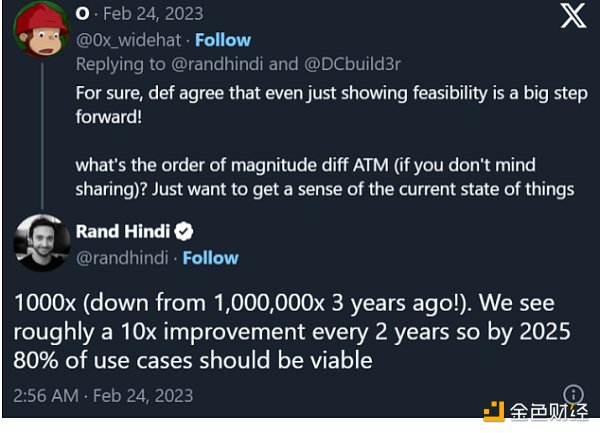
FHE的性能取决于硬件加速，在ASIC出现之前，预计价格不会便宜。

按照Leo Fan的说法，FHE的开销大约是未加密计算的10,000倍。使用GPU和FPGA可以实现比CPU高2个数量级的性能。为FHE设计ASIC可以实现3-4个数量级的性能提升（相对于CPU），几乎填平了10,000倍的价格差。”如果应用需要无交互的解决方案，那么ASIC似乎是最好的选择。由于对于一些简单的计算，如线性计算，FHE的性能和密文是令人满意的，因此GPU/FPGA加速的FHE结合MPC技术可用于一些网络连接良好的应用。

如果可以生成FHE正确执行的证明以避免执行冗余，我们就可以拥有可证明的FHE（类似于ZK）和zk-FHE-rollup。

5、FHE技术细节

（1）安全性

思考FHE的安全性，我们来假设有四方：加密者、解密者、进行FHE计算的一方和对手方。加密者和解密者可能是同一个人，那么我们要处理对称FHE。也可能存在多个加密者的情况。FHE的安全假设是所有这些参与方都可能是不诚实的。

（2）密码学

FHE是一种基于晶格点阵（lattice based）结构。最初的FHE提案是以理想的lattice为基础的，从那时起，它就显示出了不安全的一面。

什么是lattice？

Lattice是n维空间中由点组成的周期性网格。可以有无限个basis（基）。basis的长度就是其最长向量的长度。我们把最小化最长向量长度的基称为“short basis”（短基）。

短向量点阵问题（Short Vector Lattice Problem）听起来是这样的：给定一个任意basis b，找到一个尽可能短的非零点阵向量。

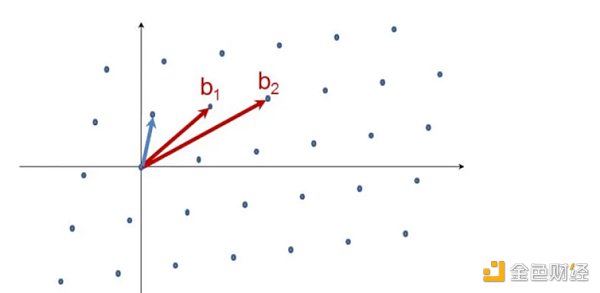
此问题的另一个版本被称为解码问题（Decoding Problem）。在这个版本中，一个人被要求在特定区域内找到一个目标点（不是最短的，但不超过某个特定值）。

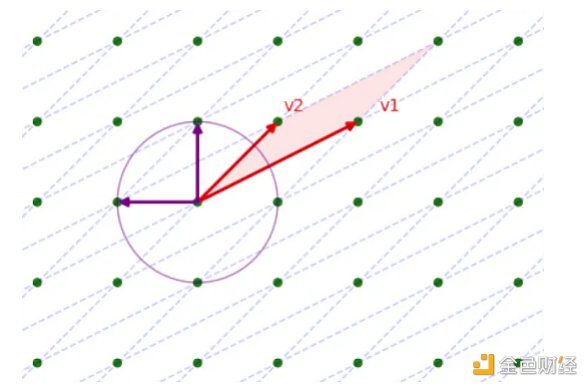
这两个问题的核心区别在于短向量问题只要求一个唯一向量。在解码问题中，在一个固定的较大半径内总会存在多个点。

如果你在二维空间中思考这个问题，就很简单：lattice就是平面上的无限个点的集合。这些点是由两个“basis向量”的整数线性组合产生的。涉及到的数学难题就是找到两个生成lattice的短向量。在下图中，黑色向量是“basis向量”，红色向量是“数学难题”的解：

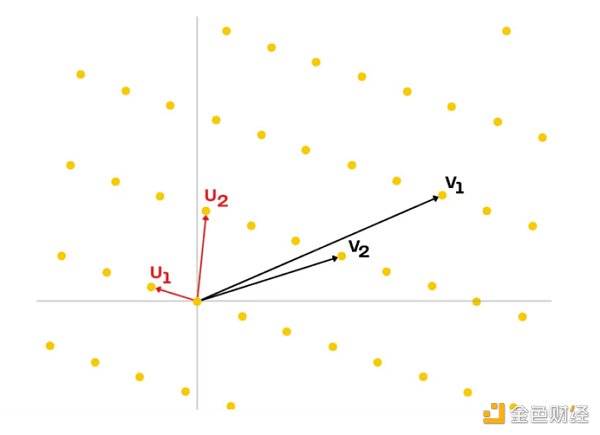
在二维空间中，这个问题看起来简单得可笑。然而，当我们将空间维度数量增加时，这个问题确实变得非常困难。尤其是复杂度随着空间维度的增加呈指数增长。对于非常多维度的空间来说，问题变得太困难，我们甚至怀疑量子计算机是否可以应对这个难题。

该问题的重要参数是精确的维度数量和初始basis向量的选择。

人们建议将Lattice作为后量子原语背后的核心机制。

许多改进的FHE方法（如FHEW、TFHE、BGV、BFV和CKKS）都是基于容错学习（LWE）的，而LWE则基于lattice问题。

6、TFHE运作机制观察

TFHE中的T代表Torus，一种类似甜甜圈的数学结构。

该方案的安全性基于一个称为LWE（容错学习）的lattice难题。

TFHE不同于其他方案，因为它推出了一种特殊的bootstrapping同态刷新，速度非常快，能够在降低噪声的同时求解函数。

Part 1：定义密文

尤其需要注意的是TFHE使用了三种类型密文：LWE、RLWE和RGSW，它们都具有不同的属性，在同态运算中非常有用。让我们来看看GLWE（Generalized LWE，包含LWE和RLWE）来简单了解这些密文。消息加密可以表示为：

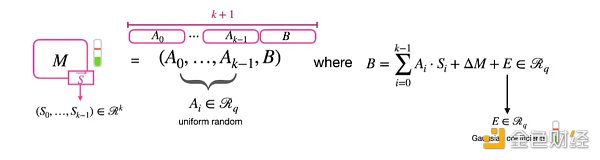
其中M为加密信息，△= q/p中q和p均为大整数（通常为2的乘方），S_i为密钥（k是最多为N次方的多项式），A_i为随机抽样系数（称为“mask”掩码），E为噪声误差。每次加密都对“mask”和噪声误差进行采样，也就是说即使对同一消息进行加密结果也会有所不同。

为了能够解密消息，|E|应该小于△/2 (|E|<△/2)。如果此条件成立，解密将如下所示：

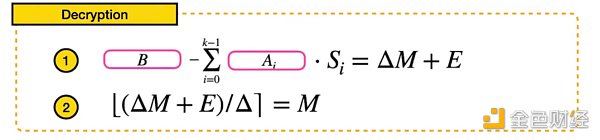
回头看bootstrapping，我们在前文简要介绍了一种降噪工具，该工具正好应用了上述两步解密过程。特别是，它在第一步中计算了单项式X的指数，然后使用这个新的单项式来轮替查找表（Look-Up Table, LUT），用来计算第二个解密步骤（重缩放和近似舍入）。

从GLWE到LWE，取N = 1（N是S中多项式的最大可能乘方）。

从GLWE到RLWE，取k = 1 （S中多项式的个数），N-2的乘方。

为了简要定义GGSW，我们必须简要定义GLev，即GLWE密文的向量。那么，GGSW密文就是GLev密文的向量。若GLWE密文是R_q元素的向量，则GGSW密文就是R_q元素的三维矩阵：

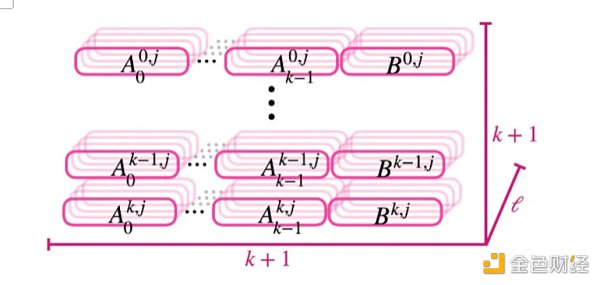
Part 2：密文同态加法的运算

假设我们有两个GLWE密文对消息M和M’进行加密。然后，我们可以将两个密文各分量相加，结果将得到一个新的GLWE密文，对M+M’的合进行了加密。

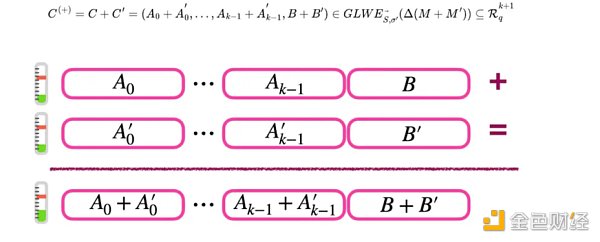
为了执行同态加法运算，我们在R_q 中谨慎添加分量项：

A₀⁽⁺⁾ = A₀ + A’₀, A₁⁽⁺⁾ = A₁ + A’₁, B⁽⁺⁾ = B + B’

Part 3：未加密常数的同态乘法运算

假设我们有一个GLWE密文加密了消息M和一个小常数多项式Λ。然后，我们可以将多项式Λ乘以密文M的每个分量，结果将是一个新的GLWE密文加密Λ⋅M的乘积。

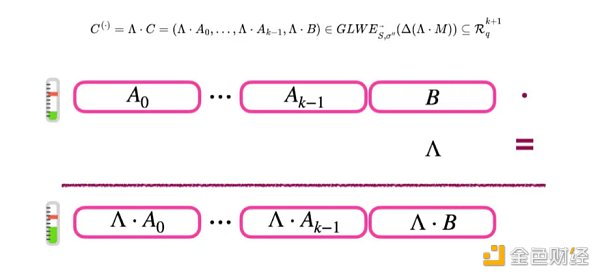
至于解密，也可以使用与GLWE相同的方法。

要将两个GLev密文或两个GGSW密文相加，只需将组成它们的对应GLWE密文相加即可。假设我们想要将GLev密文或GGSW密文乘以一个小常数多项式Λ。在这种情况下，将所有GLWE密文相加乘以Λ就足够了。

然而，这只在常数很小的情况下有效。如果常数很大，噪声就会与常数大小成比例地增长。如果我们将密文的各元素与一个较大常数相乘，噪声就会影响结果。为了解决这个问题，需将大常数分解为多个base底数：

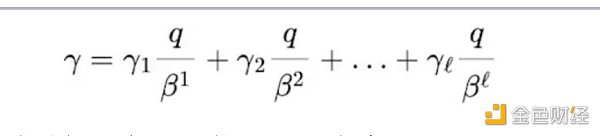
为了使分解可逆，可以使用GLev加密。

另一种选择是基于NTRU假设的方案。然而，这些方案也明显安全性不足。

目前，假设只有LWE方法是适用的，但有一个缺点，就是LWE类型加密要求每个密文由两个元素组成，而NTRU方案的主要优点是密文仅由一个ring元素组成。另一个问题是，从某种意义上说，就是把安全性的全部鸡蛋放在一个篮子里。

7、当前区块链FHE项目

Zama——隐私保护开源加密工具。

Secret Network——具有可定制隐私功能的区块链。

Sunscreen——一个用于全同态加密和零知识证明的编译器。

Fhenix——一个由全同态加密提供支持的区块链。

Ingonyma——硬件加速。

Cysic——硬件加速。

Mind Network——隐私rollup。

8、区块链外的FHE项目

FHE可应用于许多需要隐私保护计算的情况。

除了区块链项目，FHE还主要应用于注重隐私保护的机器学习。例如，客户端希望使用自己的私有数据和外部AI模型。

客户端使用FHE对数据进行加密，然后将密文上传到服务器。服务器对密文进行AI模型的同态计算。计算完成后，服务器返回加密结果，客户端可以对其进行解密查看结果。

基于FHE的安全性和功能性，客户端数据的保密性和结果的正确性可以得到保障。该应用的一个突出特性是，在计算过程中，客户端并不需要与服务器交互。

来源：金色财经