从区块链到 DAG（四）MeerDAG 共识之 GHOSTDAG 协议lg...

上一篇文章我们重点介绍了 SPECTRE 共识协议如何产生区块、如何处理冲突交易以及产生可信交易集、如何防止网络攻击的基本原理，虽然 SPECTRE 是一个支持快速确认的 blockDAG 协议。但是 SPECTRE 只能对冲突交易做一个相对排序（判断冲突交易间的先后顺序），无法给所有的区块做一个绝对排序，所以 Qitmeer Network 引入了时序性更强的 GHOSTDAG 协议，可以对整个账本做一个线性排序，有效满足了区块链网络对账本时序性的要求。

首先在设计 MeerDAG 协议之前，我们意识到必须要假设整个节点网络满足去中心化的大前提，也就是 50% 以上的节点都是诚实可靠的，才能有效的保障账本安全。可即使大部分节点都遵守挖矿规则，也不能保证每个节点都是诚实可靠的。如果有存心作恶的节点，是完全可以去记录一些虚假交易，并且屏蔽掉其他好节点的区块，达到篡改交易的目的。如果这样的话，我们如何区分哪些区块来自好节点，哪些来自坏节点呢？

正因如此，Qitmeer Network 使用了依靠 GHOSTDAG 协议判断连通度的方法来判断区块图网络的红蓝块，简单来说就是恶意节点产生的区块与诚实节点产生的区块之间的连通度比较低，反之诚实节点产生的区块之间的连通度会比较高。

其次，再定投票机制，和比特币一样， Qitmeer Network 采用的出块共识是 PoW ，用算力进行投票。但不同的是，账本共识标准不再是看哪条链最长，而是看图中哪个子集包含最多诚实节点相互联通的区块，并且满足 k 值的要求。为了更好地表述清楚，下面会把满足 k 值要求的子集称为 k-cluster。

接下来，我们可以设计分类算法，来把好节点和坏节点的区块都区分出来。既然好节点的区块集就是图中最大的 k - cluster 子集，那剩下来的部分自然就来自坏节点。所以算法的核心就是找出最大的 k - cluster 子集。

最后通过拓扑规则对区块图内所有区块进行线性排序，原则上先排诚实块，后排非诚实块，达到对所有区块建立时序性，再对诚实块进行区块奖励。但是，非诚实块并不一定就是恶意块，它们也同时参与了记账过程，所以可以获得区块交易的手续费。

GHOSTDAG 协议主要分为两个内容：

1. 通过投票判定诚实区块和恶意区块；

2. 对区块做线性排序。

下面将逐一对这两个内容进行说明。这里重申一下账本共识有效的大前提：网络中大多数节点都是诚实的。我们不考虑集中超过 51% 算力这种恶意攻击，因为无论采用的是什么账本共识，这样的攻击都会奏效。 

GHOSTDAG 的投票原则

从(《 从区块链到 DAG（三）MeerDAG 共识机制之 SPECTRE 协议技术详解 》)文章中的描述可以看出：“ 双花 ”攻击时，攻击区块在发布前几乎不会与诚实节点产生的区块相关联，因为在这个阶段，诚实区块不知道这些攻击区块的存在，所以自然不会引用它们。在 censorship 攻击中，攻击节点产生的区块也有类似的倾向：不与诚实节点所产生的包含“冲突交易”的区块相关联。

综合来看，这些恶意攻击都有一个显著特点：恶意节点产生的区块与诚实节点产生的区块之间的连通度比较低，反之诚实节点产生的区块之间的连通度会比较高。

GHOSTDAG 的投票原则正是基于这个原理，通过判断不同区块间的连通度进行投票。为了描述清楚这个投票过程，我们先介绍几个有关的概念，如图1

* 图1 一个典型的 DAG 图例

来源：Yonatan Sompolinsky, Shai Wyborski, and Aviv Zohar，⟪ PHANTOM and GHOSTDAG：A Scalable Generalization of Nakamoto Consensus ⟫

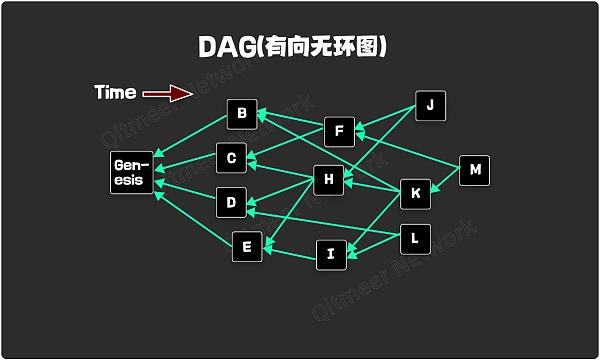
以区块 H 作为例：past ( H ) = { Genesis, C, D, E } - 在 H 创建之前直接或间接指向 H 的过去区块 future ( H ) = { J, K, M } - 在 H 创建之后直接或间接指向 H 的未来区块。anticone ( H ) = { B, F, I, L } - 除开 past ( H )，future ( H ) 之外的区块，这些区块与 H 并没有直接或间接的指向关系。如何对这些区块的排序是 DAG 共识的主要难点。tips ( G ) = { J, L, M } - 树叶区块，或者末端区块；这些区块会成为新区块的块头引用。

分叉系数 k，直观上看这是一个描述网络允许分叉的个数。严格来说 k 被定义为传播系数（ propagation parameter )，用来描述网络延迟（ propagation delay ）这个现象。在（《 从区块链到 DAG（一）账本结构和共识机制 》）的文章中有描述过，在实际过程中网络延迟的现象无法避免，而这种延迟会导致分叉。想要避免分叉，就要保证在网络延迟的时间段 Δt内不产生新的区块，即（ k = 0）。k 值的定义非常重要，当 k 值太大时会使分叉过多，降低网络的安全性；当k 值太小时又会限制网络性能，使 Tps 较低，比如区块链就是一种 k = 0 的网络。连通度的高低是通过 k 值来判定的，区块的连通度要满足最大 k - cluster 的子集要求，如图2

* 图2 k - cluster 子集要满足的条件

来源：Yonatan Sompolinsky, Shai Wyborski, and Aviv Zohar，⟪ PHANTOM and GHOSTDAG：A Scalable Generalization of Nakamoto Consensus ⟫

如何判断一个区块是诚实节点产生的呢？先找到这个区块的 anticone 的集合，这个集合和 DAG 的 k - cluster 的子集 S 的交集数目，如果小于或等于 k ，则这个区块是诚实节点产生的，会被加入到子集 S ，反之则是攻击节点产生的区块，不会加入集合。当迭代整个过程把全部区块滤过一遍以后，所有被判断为诚实的区块都会加入这个子集 S ，这时候的 S 被称为最大的 k - cluster 子集，写做 MSCk，集合里的所有区块会被计入账本。

* 图3 一个最大子集为 3 - cluster 的 DAG 图例，k = 3

来源：Yonatan Sompolinsky, Shai Wyborski, and Aviv Zohar，⟪ PHANTOM and GHOSTDAG：A Scalable Generalization of Nakamoto Consensus ⟫

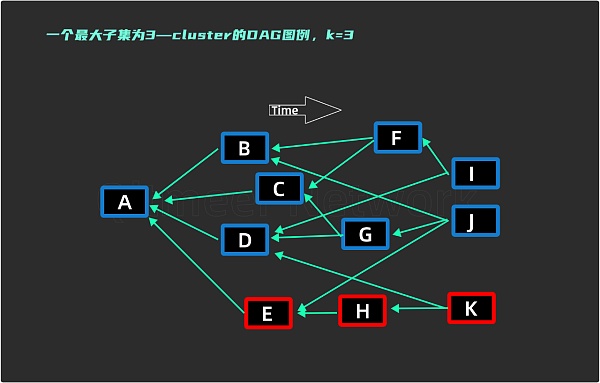
如图3 所示，诚实节点产生的区块标记为蓝色，攻击节点产生的区块标记为红色。所有满足图2 要求的集合都属于 3 - cluster 的最大子集，也就是所有的蓝色区块都属于 MSC3。我们来验证一下是否这样的区块划分能符合上述要求。

蓝色区块以 G 为例：anticone ( G ) = { B, F, I, E, H, K }; anticone ( G ) 与蓝色区块的交集是 B, F, I ，共 3 个，满足小于等于 k 值的要求（ 该 DAG 的 k 值为 3 ），故 G 是诚实节点产生的区块，可以被计入账本。所有的蓝色区块都满足这一要求。

红色区块以 E 为例：anticone ( E ) = { B, C, D, F, G, I }; anticone ( E ) 与蓝色区块的交集是 B, C, D, F, G, I，共有 6 个，大于这里的 k 值 3，所以 E 则被判断为攻击节点产生的区块，不会被计入账本。所有的红色区块也都符合这一原则。

依照这个规律依次滤过所有区块就可以判断和排除攻击区块，这背后的原理很简单：区块 X 的 anticone ( X ) 是指与 X 无关的区块的集合，若 anticone ( X ) 与诚实节点产生的区块交集越多，则代表 X 与诚实区块的连通度越低，这里通过给连通度加上一个极限值 k 作为判断标准：若 anticone ( X ) 与诚实区块交集数高于 k 值，代表 X 区块与诚实区块的连通度低，X 会被判断为攻击区块；反之则代表 X 与诚实区块的连通度高，X 被认为是诚实区块。 

线性排序

拓扑排序的定义：对一个有向无环图 ( Directed Acyclic Graph 简称 DAG ) G 进行拓扑排序，是将 G 中所有顶点排成一个线性序列，使得图中任意一对顶点 u 和 v ，若边 < u , v > ∈ E ( G )，则 u 在线性序列中出现在 v 之前。通常，这样的线性序列称为满足拓扑次序 ( Topological Order )的序列，简称拓扑序列。

简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

这个过程总结起来有三个要点：1.有向无环图；2.序列里的每一个点只能出现一次；3.任何一对 u 和 v ，u 总在 v 之前（这里的两个字母分别表示的是一条线段的两个端点，u 表示起点，v 表示终点 ）。

按照判断红蓝块的原理，找到 MSCk 子集以后，下一步就是对集合里的进行线性排序，排序的原则和拓扑排序一样，如图4

*图4 拓扑排序

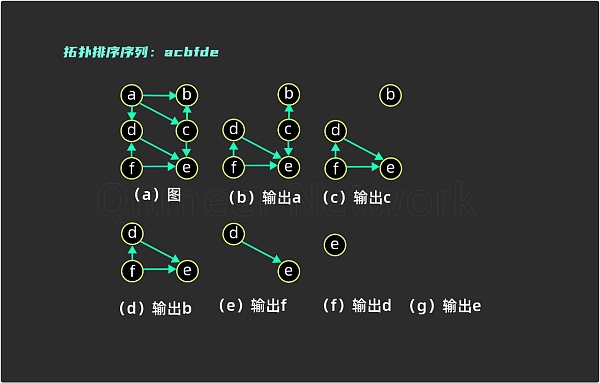
拓扑排序是指把 DAG 上的顶点排列成一个线性序列，由集合上的一个偏序得到该集合的一个全序的过程。排序的原则：优先选取没有箭头输入的顶点为起点，每排完一个序列就把这个顶点从图中移除，再从移除后的图中选取没有输入的顶点作为下一个序列，如此循坏直到最后一个顶点被输出。需要注意，拓扑排序的顺序并不是唯一的，可能存在多种选择方案，如图4 也可以在 ( c ) 步骤选择输出 f , 最终顺序为 acfbde 。根据这个原则，图3 中的 DAG 最终的输出结果之一是：A ->D ->C ->G ->B ->F ->I ->E ->J ->H ->K 。这个结果可以是任意的拓扑排序，但是蓝色区块会优先排列，红色区块由于连通度低会自然的排在蓝色区块后面。 

GHOSTDAG 协议的应用举例

由上文可知，GHOSTDAG 协议的第一步是判断诚实区块，也是最关键最复杂的一步，如何高效确定 MSCk 将直接影响全网的性能。这里引入贪心算法来解决这个问题，先根据每个区块的连通度（区块 past ( ) 集合里的元素个数）来打分，选出总分最大的区块组成主链，这些区块会组成最初的子集 S ，剩下的区块将依照主链的顺序依次投票选出。原理是入选主链区块都有着较高的连通度，可以优先加入 S 集合。这样整个网络会按照连通度从高到低的趋势去投票，用最快的方式找到最大的 k - cluster 子集 MSCk 。下面我们通过一个例子来完成复盘一下 GHOSTDAG 协议的运作过程：

* 图5 GHOSTDAG 协议在一个 k = 3 的 DAG 图中的应用示例（ 第一步 ）

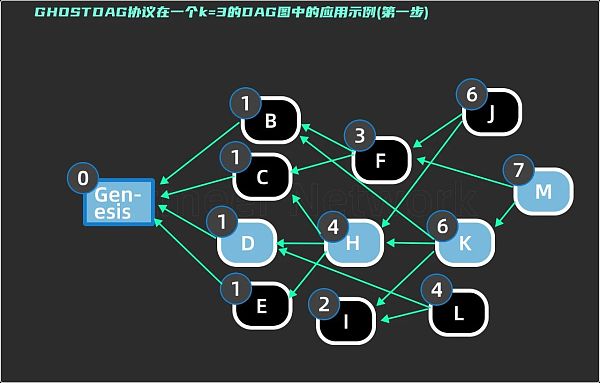
来源：Yonatan Sompolinsky, Shai Wyborski, and Aviv Zohar，⟪ PHANTOM and GHOSTDAG：A Scalable Generalization of Nakamoto Consensus ⟫

图中蓝色小圆圈中的数字代表每个区块 X 的连通度打分，分数和每个区块 past ( X ) 里的区块数目相等。根据贪心算法的规则，我们需要选出一条总分最高的路径，先选出分值最高的区块 M , 然后依次向前滤过 M 的所有过去区块 past ( M ) ，如果遇到两个区块分值相等，则随机选择一条路径，最后选出的主链路径。如图5 中蓝色区块所示：Gensis ->D ->H >K ->M，最初的 S = { Genesis , D, H, K, M } 。接下来验证：D 区块 past ( D ) 只有创世区块，anticone ( Genesis ) 是个空集，与 S 的交集个数为 0 ≤ 3 ，所以创世区块满足 3 - cluster 的子集要求，用蓝色边框标注。

* 图6 GHOSTDAG 协议在一个 k = 3 的 DAG 图中的应用示例（ 第二步 ）

来源：Yonatan Sompolinsky, Shai Wyborski, and Aviv Zohar，⟪ PHANTOM and GHOSTDAG：A Scalable Generalization of Nakamoto Consensus ⟫

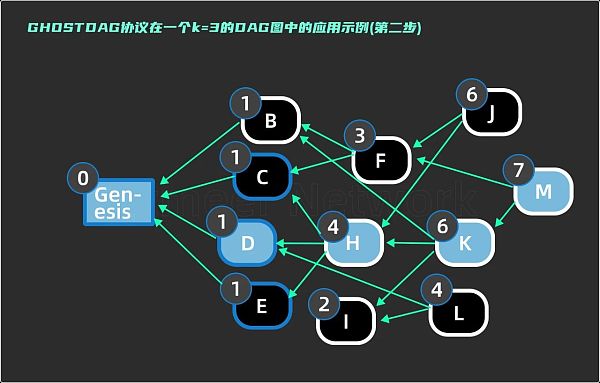
第二步，来到区块 H ，past ( H ) 除了创世区块以外还有 C, D, E, 分别找到这三个区块的 anticone 集合并判断它们与 S 之间的交集个数是否小于等于 k 值，这里 k 值为 3 。anticone ( C ) = { B, D, E, I, L }; 与 S 的交集是 { D }，交集个数为 1 ≤ 3。anticone ( D ) = { B, C, F, E, I, L }; 与 S 的交集个数为 0 ≤ 3。anticone ( E ) = { B, C, D, F }; 与 S 的交集交集是 { D }，交集个数为 1 ≤ 3。因此这三个区块都加入到 3 - cluster 的子集中，这一步结束时子集更新为 S = { Genesis , D, H, K, M, C, E }，在图6 中用蓝色边框标注。

* 图7 GHOSTDAG 协议在一个 k = 3 的 DAG 图中的应用示例（ 第三步 ）

来源：Yonatan Sompolinsky, Shai Wyborski, and Aviv Zohar，⟪ PHANTOM and GHOSTDAG：A Scalable Generalization of Nakamoto Consensus ⟫

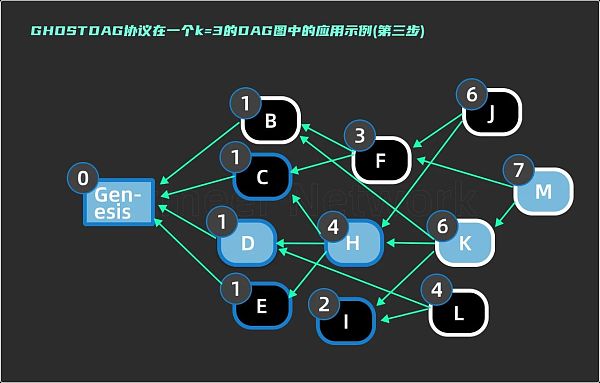
第三步，访问区块 K ，past ( K ) 中需要判断 H, I, B，是否要加入子集 S 。anticone ( H) = { B, F, I, L }; 与 S 的交集个数为 0 ≤ 3。anticone ( I ) = { B, C, D, H, F, J }; 与 S 的交集为 { C, D, H }，交集个数为 3 ≤ 3。所以在这一步结束时 H 和 I 也要加入 S，在图7 中用蓝色边框标注。anticone ( B ) = { C, D, E, H, I, L }；与 S 的交集为 { C, D, E, H }，交集个数为 4 > 3。所以 B 不满足 3 - cluster 的子集条件，不会被加入到子集中，B 被判定为恶意节点产生的区块。第三步结束时，子集更新为 S = { Genesis , D, H, K, M, C, E, I }。

* 图8 GHOSTDAG 协议在一个 k = 3 的 DAG 图中的应用示例（ 第四步 ）

来源：Yonatan Sompolinsky, Shai Wyborski, and Aviv Zohar，⟪ PHANTOM and GHOSTDAG：A Scalable Generalization of Nakamoto Consensus ⟫

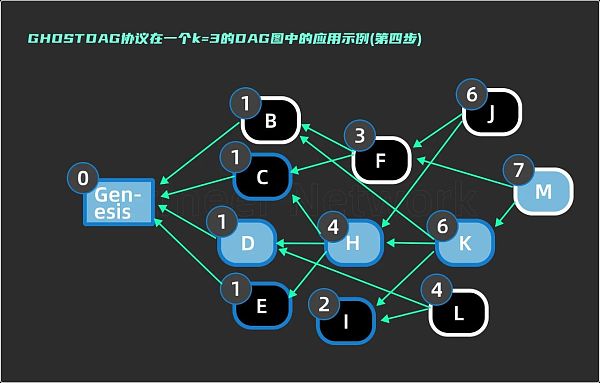
第四步，访问区块 M，past(M)中需要判断 F, K 是否要加入子集 S。anticone ( K ) = { F, J, L }; 与 S 的交集个数为 0 ≤ 3。anticone ( F ) = { D, H, K, E, I, L }；与 S 的交集为 { D, H, K, E, I }，交集个数为 5 > 3 。所以区块 K 被加入到子集，而 F 不被加入。这里更新子集 S = { Genesis, D, H, K, M, C, E, I }。

* 图9 GHOSTDAG 协议在一个 k=3 的 DAG 图中的应用示例（ 第五步 ）

来源：Yonatan Sompolinsky, Shai Wyborski, and Aviv Zohar，⟪ PHANTOM and GHOSTDAG：A Scalable Generalization of Nakamoto Consensus ⟫

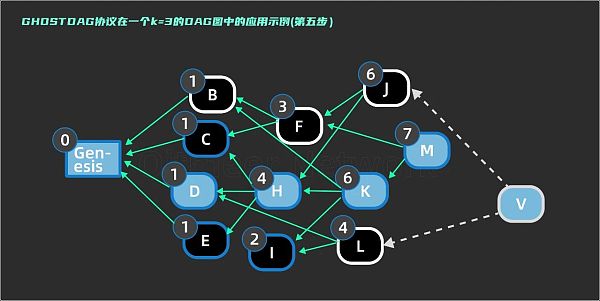
最后一步（第五步），访问到一个还没正式产生的虚拟区块 V ，V 引用的区块是 tips ( G ) ，这意味着 past ( V ) 是整个现有所有区块，在图9 中用虚线表示。继续判断 J, M, L 是否加入子集。anticone ( M ) = { J, L }; 与 S 的交集个数为 0 ≤ 3。anticone ( L ) = { B, C, F, J, M, H, K }；与 S 的交集为 { C, M, H, K }，交集个数为 4 > 3, L 不属于 3 - cluster 的子集。anticone ( J ) = { M, K, I, L }; 与 S 的交集为 { M, K, I }，交集个数为 3 ≤ 3；按理说 J 应该加入子集，但是这会导致 anticone ( I ) 最终与最大子集 MSC3 的交集变为 { C, D, H, J }，交集个数 4 > 3 ，I 不能被加入到子集集合中。这会得到一个与前面步骤相矛盾的结果，所以这里不能把 J 加入子集。最终这个 DAG 图的最大 3 - cluster 的子集 MSC3 = { Genesis, D, H, K, M, C, E, I }。

接下来我们开始排序：先对 MSC3 中的蓝色区块做拓扑排序 Genesis ->D ->E ->C ->I ->H ->K ->M。然后对不在 MSC3 中的黑色边框区块排序，再添加到蓝色区块的排列之后，最终排序为 Genesis ->D ->E ->C ->I ->H ->K ->M ->B ->F ->L ->J。交易在每个区块内部会自动按照它们的出现顺序排序，至此，整个网络的线性排序就完成了。 

DAG 结构难度调整

无关区块极限值（ k 值 ）的定义非常重要，因为连通度的高低是通过 k 值来判定的，如果 k 值太大会使分叉过多，导致缓慢的确认时间，同时红色块的比例也会升高，降低网络的安全性；如果太小又会限制网络性能，使 Tps 较低。如何兼顾网络效率和安全性成为摆在 Qitmeer Team 面前的问题。

MeerDAG 结构难度调整主要是通过控制出块时间和无关区块极限值（ k 值）来进行的：（1）让出块按照目标时间进行产块；（2）根据并发数限制让每个难度上的并发数按照预设参数进行。

按照区块为 1M 的标准尺寸来说，当前的互联网环境，大致需要 10 秒可以广播到 90% 以上的节点，一般 15 秒以内区块可以传遍绝大多数节点。对于新生网络，由于区块交易较少，加上节点分布较为集中，15 秒更是几乎足够可以传遍所有节点。但是总有例外的情况造成节点没有在 15 秒内同步区块，我们把这些没有同步的区块统称为失效区块，也就是红色区块，其他的正常区块自然就是蓝色区块。

通过设置并发数限制的影响参数，出块率、安全等级、区块传播时间，来控制无关区块极限值（ k 值 ）。区块传播时间是指区块传播到全网的最大时间，保证了容错能力。安全等级是指有多大概率一个诚实的区块会被判定为无效区块，即红色区块，或者也可以理解为网络的容错能力。出块率就是每秒产生的区块数。安全等级和传播时间可以认为是网络的物理属性，能用经验值或者测算出来，可以认为是常量，而出块率则是网络的参数，可根据网络运营的需要进行调整。

Qitmeer Team 通过对出块率、安全等级、区块传播时间的不同参数设置和测试来判断最佳的出块时间和无关区块极限值（ k 值 ），最后发现安全等级采用 1%，区块传播时间为 30 秒，出块率为 1/30（ 块/秒 ）的设置最为适合：

~/github.com/forchain/AnticoneSize ( master * ) $ . / AnticoneSize - rate 0.03333333333 delay : 15 rate : 0.03333333333 _ security : 0.01 expect : 0.9999999999 coef : 0.3678794412082303k = 0 sum = 0.6321205587917698；k = 1 sum = 0.2642411176203274；k = 2 sum = 0.08030139705300021；k = 3 sum = 0.01898815687002247；k = 4 sum = 0.0036598468258108655.

通过上述参数的测试结果可以看到，无关区块超过 4 个块的概率只有 0.366% ，超过 1 个块的概率只有 26.42% ，即大多数情况下，要么就是一条链，要么就只有一个侧链区块。这样首先确保了 k 值大部分时间保持在可控范围内，这样红色块的比例可以有效降低，同时也是出于对经济模型设计和账本膨胀的考虑，等到后续链上生态繁荣后，还可以通过降低出块时间来大幅度提高网络性能，保障对性能需求较高的业务场景的落地。 

总结

当 k = 0 时，GHOSTDAG 的规则就表现为比特币的最长链共识，和 SPECTRE 协议一样，GHOSTDAG 协议是最长链共识的拓展。与 SPECTRE 的不同之处在于 GHOSTDAG 这种可以严格排序的账本共识，适用于有线性排序要求的网络，同时解决了 SPECTRE 协议交易弱活性的问题。

Qitmeer Network 是少数采用 SPECTRE + GHOSTDAG 这两种协议的 blockDAG 混合共识的高性能公有链。虽然这两个协议的安全性已经在数学理论上得到了验证，但是受限于在代码层面的实现难度和 blockDAG 理论研究的迟缓，目前已经落地应用的项目并不多，例如 Conflux、Kaspa、Qitmeer、Xdag 等项目都是 blockDAG 的技术先驱。

Qitmeer Team 在 18 年选型确定采用 blockDAG 共识，19 年初设计出 MeerDAG 技术原型，前后经过长达 18 个月真实算力测试环境，在持续优化 MeerDAG 共识的同时不断演进挖矿算法，终于在 21年9月30号正式上线主网。

Qitmeer Network 已于2022年与英国伯明翰城市大学联合成立了 MeerLabs 区块链技术研究实验室，专注于区块链底层技术的学术研究，以及区块链新媒体的发展方向。实验室内聚集了 DAG 领域内专家学者，就区块链技术研发、商业应用、产业战略等方面进行深入研究。我们期待在未来， blockDAG 理论研究和 Qitmeer Network 生态的扩展上会有更进一步的发展。 

参考资料

[1] GHOST, DAG, SPECTRE, PHANTOM 和 CONFLUX 技术原理

[2] Yonatan Sompolinsky, Shai Wyborski, and Aviv Zohar， ⟪ PHANTOM and GHOSTDAG ：A Scalable Generalization of Nakamoto Consensus ⟫

[3] 共识算法解读：泛化的中本聪共识 PHANTOM

[4] DAG 的妙用（三）比特币协议的扩展

[5] CSDN 博主「 CorLeoneEF 」

[6] Yonatan Sompolinsky, Yoad Lewenberg, and Aviv Zohar， ⟪ SPECTRE：Serialization of Proof-of-work Events: Confifirming Transactions viaRecursive Elections ⟫

[7] Qitmeer Team：《Qitmeer 中文白皮书》

来源：金色财经