撰文：Fox Tech CTO 林彦熹，Fox Tech 首席科学家 孟铉济

前言

Prover和Verifier之间的计算代理思想是零知识证明的核心内容之一，是调节证明者和验证者工作量于复杂度之间取舍（trade-off）的工具。不同的零知识证明算法本质的不同在于不同程度的计算代理；高度的代理虽然会使验证的计算容易，但是却可能使得证明的复杂度高，从而导致证明耗时长，或是生成的证明大小较大；反之，低程度的代理会使得验证者的开销较大。

图1: 零知识证明的计算代理程度影响

计算代理是什么

随着以太坊上应用和用户的扩展，以太主网上的拥堵程度不断提升，使用zkRollup进行Layer2的扩容成为一个很有吸引力的方案，FOX就是专注于使用FOAKS算法进行zkRollup的项目。而zkRollup的可行性，本质上在于使用的零知识证明算法的原理可行性。简单来说，零知识证明算法实现的功能是使得证明者向验证者证明某件事，但又不透露任何关于这件事的信息。zkRollup的构造就是利用了这个性质，使得Layer2的节点可以执行原本在Layer1进行的计算，同时向Layer1节点提供计算正确性的证明。

从更广义的角度来说，上述的过程我们可以理解为，由于验证者（Layer1节点）计算能力有限，所以将这部分的计算代理给了证明者（Layer2节点）来执行，证明者完成了这个任务，需要返回结果给验证者。从这个角度来说，我们可以说，零知识证明算法使得保障正确性的“计算代理”得以实现。从宏观上这种计算代理的例子可以表现为zkRollup这种形式的应用，具体到零知识算法当中，这种计算代理的思想也有各种应用。

本文主要介绍FOAKS使用的在Orion当中提到的Code-Switching所做的令证明者帮助验证者执行的验证计算过程，以及FOAKS如何应用这种技巧进行递归。从而减少了证明的大小以及验证者的开销。

为什么需要计算代理

从系统的实用性角度来说，很多情况下计算节点的算力是有限的，或者说计算资源是很宝贵的。例如在Layer1链上的所有计算（包括转账以及合约调用）都需要经过所有节点的共识，并且用户需要为此支付高昂的手续费。所以，在这种情况下，将本来由共识节点来处理的计算“代理出去”交给链下节点来完成，就是一种自然的想法，避免消耗链上资源。而这也正是FOX所专注的链下计算服务。

从密码学理论角度来讲，在GMR模型当中限定了证明者拥有无限计算能力，验证者拥有多项式计算能力。如果验证者也有无限能力，则零知识证明的基本性质无法满足。所以自然地，将计算向证明者一方倾斜，让证明者承担更多的计算就是很多零知识证明算法设计都会考虑的问题。

当然，为了实现这一点，我们需要特别的技巧。

Code Switching

这一节介绍Orion当中使用的Code Switching技巧。Orion和FOAKS都使用了Brakedown作为多项式承诺方案，而Code Switching是在Orion当中命名的有证明者代替验证者执行验证计算的过程。

在《一文了解FOAKS当中的多项式承诺协议Brakedown》一文当中我们曾经介绍过，验证者的验证计算为以下的过程:

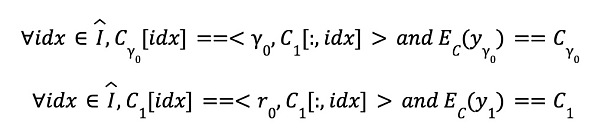
现在如果令证明者承担这部分计算，则证明者除了执行这些计算，还要附上证明值来证明自己的计算是正确的。

做法是将上述等式同样写成R1CS电路：

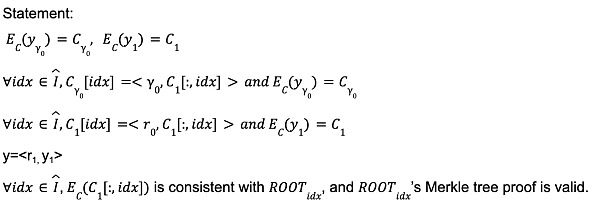
之后使用Virgo算法进行验证。

FOAKS当中的计算代理

在FOAKS当中同样使用类似的技巧完成计算代理，值得一提的是，FOAKS由于使用了Fiat-Shamir heuristic技巧实现了非交互式证明。想要了解更多，读者可以参考《如何将交互式证明改造为非交互式？Fiat-Shamir Heuristic！》。所以FOAKS的挑战生成和Orion所使用的Code Switching方法不同，电路当中也需要加入新的等式：

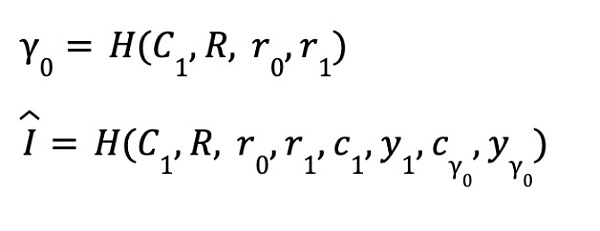
这样之后FOAKS当中的证明者同样生成了代理验证者进行验证的计算证明。而对于验证证明的过程，FOAKS利用算法自身进行迭代，这也是FOAKS实现递归的关键内容。具体内容见《如何设计出一种精妙绝伦的证明递归方案》。

通过一定次数的迭代可以使得证明的大小被压缩，从而极大降低验证者的计算负担以及通信复杂度。这就是FOAKS这个零知识证明方案对FOX这条zkRollup的重大意义。

结语

zkRollup中使用的零知识证明算法的计算代理程度需要被精心设计，必须恰到好处才能使其整体达到最佳效率。而FOAKS算法通过自身迭代的递归实现了可以调节的计算代理，是为专门为zkRollup所设计的零知识证明算法。

参考文献

1.Orion： Xie, Tiancheng, Yupeng Zhang, and Dawn Song. "Orion: Zero knowledge proof with linear prover time." Advances in Cryptology–CRYPTO 2022: 42nd Annual International Cryptology Conference, CRYPTO 2022, Santa Barbara, CA, USA, August 15–18, 2022, Proceedings, Part IV. Cham: Springer Nature Switzerland, 2022.

来源：金色财经