Filecoin检索 土星Saturn奖励模拟（连载3）lg...

前面我们讲了Saturn奖励设计，请浏览“FIL检索网络土星Saturn奖励分配”，今天我们就来模拟一下Saturn奖励。

公平分配奖励（L1节点）

该分析的主要目标是比较不同的评分函数如何影响单个时期内 L1 节点运营商之间的奖励分配。在整个分析过程中，我们假设我们有 1000 个 L1 运营商，我们使用特定的统计分布生成他们的服务指标。下图显示了生成的三个服务指标的直方图——总带宽、同时超过速度阈值的请求比率（即 TTFB 和下载时间）以及正常运行时间百分比。

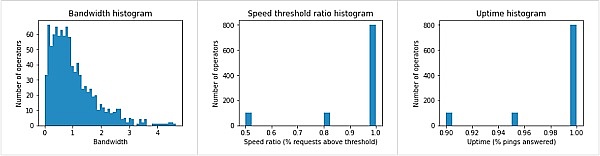
使用这些随机生成的服务指标，我们测试了不同的评分函数，即：

1、线性组合：平衡线性 - 单独的线性评分函数（指数）+ 在三个服务之间平均分配的线性组合k=1

• 平衡次线性 - 单独的次线性评分函数 + 线性组合在三种服务之间平均分配

• Balanced supra-linear - 单独的超线性评分函数 + 线性组合在三个服务之间平均分配

• 高带宽线性 - 单独的线性评分函数 + 具有更高带宽权重的线性组合

• 高带宽次线性 - 单独的次线性评分函数 + 具有更高带宽权重的线性组合

• 高带宽超线性 - 单独的超线性评分函数 + 具有更高带宽权重的线性组合

2、直接乘法：三个指标的所有次线性 - 次线性指数k=0.5

• 三个指标的所有线性 - 线性指数k=1

• 三个指标的所有超线性 - 超线性指数k=2

• 带宽平滑 - 带宽的线性指数 ( ) 和其余两个指标的次线性指数 ( )k=1k=0.5

对于每个评分函数，我们计算了单个时期内 1000 个节点运营商中每个节点的奖励分布。请注意，这里我们假设要分配的总奖励为R=100 。

这里的第一个结论是，评分函数的选择对节点运营商之间的整体奖励分配有重大影响。下表通过报告支付给单个运营商的最低和最高奖励以及基尼指数来说明这一点。回想一下，基尼指数是衡量统计离散度的指标，代表一个群体内的财富不平等。它在 0 和 1 之间变化，0 表示完全平等，1 表示最大不平等。

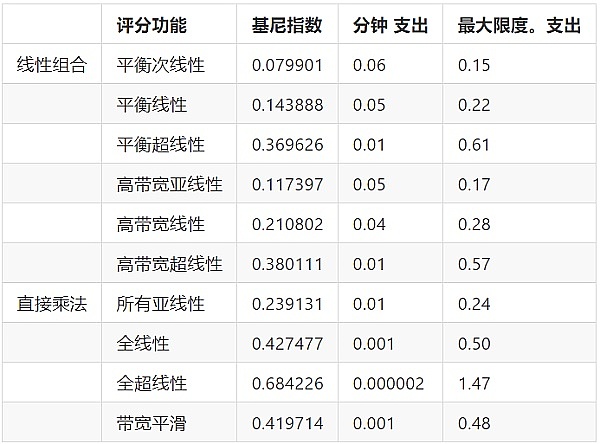
正如预期的那样，次线性函数导致奖励分配的最高平等，而超线性函数导致奖励支出的最高不平等。换句话说，通过超线性函数，我们以牺牲低绩效者为代价来奖励高绩效者。

此外，与线性组合函数相比，直接乘法函数往往会导致高绩效者获得更高的奖励集中度。唯一的例外是全次线性，它的基尼系数低于线性组合组中两个最集中的函数。

线性组合和直接乘法函数之间的动力学还有另一个不同之处，这在接下来的两个图中进行了说明。在这里，我们看到每个节点运营商根据他们提供的带宽份额获得的总支出。

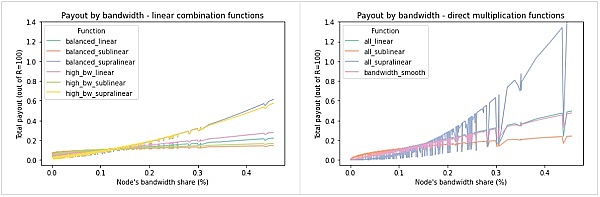
我们再次确认指数k对奖励分布的影响——在超线性函数中，奖励份额的增长速度快于带宽份额，而储备则发生在次线性函数中。

然而，这里有趣的观察是线性函数在多大程度上消除了带宽以外其他指标的不良表现。换句话说，与直接乘法函数相比，线性函数的节点因速度和/或正常运行时间性能不佳而获得的奖励下降要低得多。这种效果在所有超线性评分函数中最为突出，下载速度或正常运行时间的较低性能导致奖励显着减少。

这是一个非常相关的机制，因为我们激励节点在所有指标上都表现出色，同时对任何性能下降进行严厉惩罚。请注意，带宽平滑遵循与全线性相同的趋势，但由于速度和正常运行时间指标获得次线性指数，因此性能不佳的“惩罚”被平滑了。

激励诚实

在设置不诚实的惩罚时，需要考虑两个主要指标——真阳性率（即检测到作弊者的概率）和假阳性率（即诚实节点被标记为作弊者的概率） ). 这两个指标都需要通过过去检测到的已知案例进行估算。

如果我们有这两个指标，那么我们可以使用两个主要假设来定义应用于单个节点的惩罚调整的界限：

1、下限假设——惩罚应该足够大，这样作弊在经济上就没有优势。换句话说，作弊的预期奖励（考虑到检测概率）需要为负。

2、上限假设——惩罚应该足够小，这样它就不会对诚实节点造成太大的伤害。换句话说，诚实节点获得的期望奖励应该高于总奖励的一定百分比。

导出下限

导出上限

边界估计

在本节中，我们绘制了上面得出的惩罚调整，假设真阳性率α 、假阳性率β和最小奖励率τ的值范围. 请注意，惩罚调整是一个固定数，乘以每个节点的平均奖励（不包括惩罚）。

下图显示了获得的值：

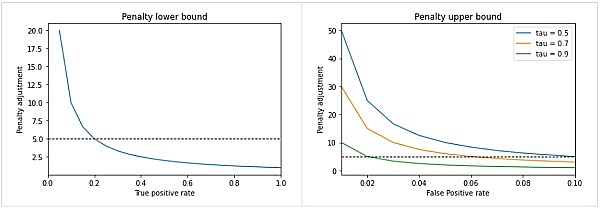
如我们所见，满足两个界限的惩罚调整的窗口有限。另外，检测系统越差（即真阳性率越低，假阳性率越高），这个窗口就越小。事实上，这些曲线已经给出了我们检测系统应该达到的一些目标，即假阳性率低于5%，真阳性率高于25%。

另一个考虑因素是惩罚需要大于 1（即需要大于每次支付的平均奖励）。这是直观的，因为如果不是这种情况，不诚实的节点总会赚到一些钱，因为没有检测系统会捕获所有的虚假日志。然而，这在不需要抵押品的情况下会产生问题——如果一个节点被标记，并且它被分配了负奖励，那么这些钱从哪里来？

一种可能的解决方案是对奖励引入一些延迟。当节点提交日志时，会计算奖励并存储一段时间。如果与此同时，该节点受到惩罚，将从存储的奖励中扣除。最后，每天“归属”的奖励将被发送到节点，减去应用的惩罚。因此，在每个时间点，所有节点都有“风险”资金，可以削减这些资金以支付罚款。

全仿真（设置最终参数）

我们希望通过最终模拟回答三个主要问题，即：

1、给定土星上要分配的新资金池，该池应如何随时间分配？特别是，我们测试了两个选项——常量池和增长池（更多细节将在专门的小节中介绍）

2、最终的评分函数应该是什么？假设我们使用直接乘法函数，带宽的指数和速度性能和正常运行时间的指数应该是多少？

3、最终的惩罚乘数应该是多少，它是否按预期工作？

我们将在其专门的小节中分析每个问题。但是，结果来自使用一些常见假设的模拟：

• 模拟时间：6个月

• 支付频率：每天一次

• 初始奖励池投资：6 个月 60 万美元（或以当前 5 美元的价格计算 12 万 FIL）。请注意，这可能不是最终可用的 FIL 池，而只是为了模拟而做出的假设。

• 初始运算符集：50

• 新运营商流入（即新运营商入网）：每天5家

• 运算符类型：

• 诚实的高性能 L1 操作员（所有操作员的 10%）：

• 每天的带宽服从正态分布，平均值为 1.2 TB，标准差为 0.1 TB

• 速比为100%

• 正常运行时间为 100%

• 被日志检测模块标记的概率为 1%（误报率）

• 诚实的平均 L1 操作员（所有操作员的 75%）：

• 每天的带宽服从正态分布，平均值为 0.9 TB，标准差为 0.1 TB

• 速比为90%

• 正常运行时间为 100%

• 被日志检测模块标记的概率为 1%（误报率）

• 诚实的低绩效 L1 运营商（所有运营商的 10%）：

• 每天的带宽服从正态分布，均值为 0.6 TB，标准差为 0.1 TB

• 速比为50%

• 正常运行时间为 90%

• 被日志检测模块标记的概率为 1%（误报率）

• 作弊的 L1 运营商（占所有运营商的 5%）：

• 每天的带宽服从正态分布，平均值为 1.2 TB，标准差为 0.1 TB

• 速比为100%

• 正常运行时间为 100%

• 被日志检测模块标记的概率为 25%（真阳性率）

奖励池

在奖励池方面，我们测试了两种不同的策略。第一个是常量奖励池，这是按时间划分奖励池的最简单和最明显的方式。特别是，我们选择了总矿池（即 120k FIL）并将其除以我们预计矿池平息网络的天数（\(个月天），即导致每日固定池为 667 FIL。30×630×6=180=180

第二种策略是增长奖励池，旨在根据网络的增长情况分配奖励。这个想法是在每个时间点都有一个网络增长的基线（在这种情况下，交付的总带宽），并在网络达到定义的基线时增加可用的奖励池。

更具体地说，给定以下变量：

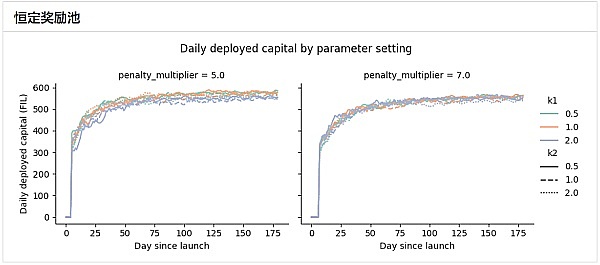
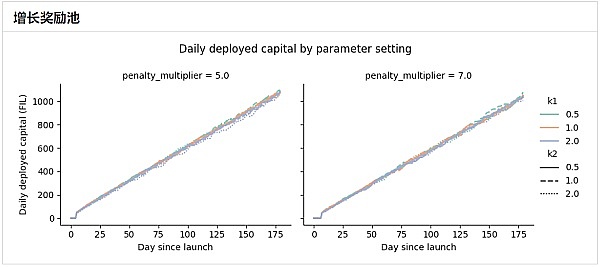
正如预期的那样，恒定奖励池相当稳定，按照设计每天支付固定数量的 FIL。围绕这个趋势的随机变化来自日志检测系统检测到的操作员的正常变化。

另一方面，增长奖励池在每日支付的总奖励方面呈线性增长趋势。这与运营商的模拟行为一致，每天都有新的运营商流入，因此观察到服务总带宽的增长。

在这两种情况下，每日部署的资金都需要几天时间才能达到稳定趋势。这是由于为建立新运营商的抵押品余额而扣留奖励造成的。

同样重要的是要注意，评分函数似乎对每日部署资本没有有意义的影响，而惩罚乘数确实有影响。这是意料之中的，因为更高的惩罚乘数会导致更高的总体惩罚，从而导致更低的总奖励。

接下来的两个图显示了平均支付给单个操作员的每日奖励（按操作员类型划分）。

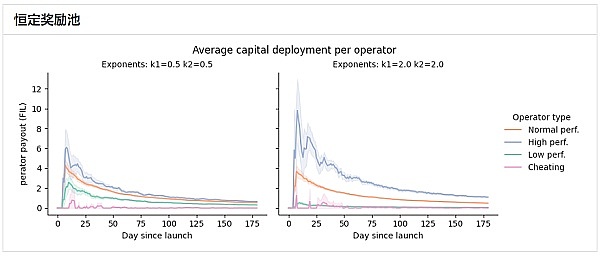
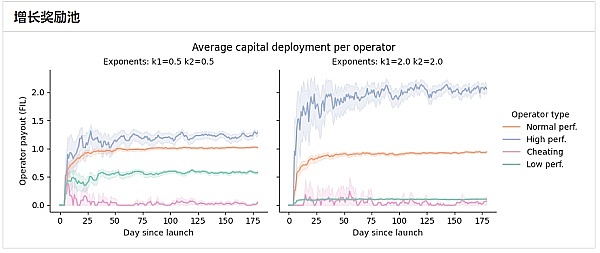
现在我们可以清楚地看到增长奖励池相对于恒定奖励池的优势——随着网络的增长和新运营商的加入，恒定奖励池导致参与者获得更小奖励的负和博弈。这会导致不良激励，即运营商因让新运营商加入网络而直接处于不利地位。

另一方面，增长池不会受到这种奖励衰减的影响，在网络启动的第一天后，支付给每个运营商的平均奖励保持相当稳定。出于这个原因，我们建议在恒定奖励池上使用增长奖励池机制。因此，对于剩余的分析，我们将重点关注使用该策略获得的结果。

我们应该注意到，如果网络以比基线更快的速度增长，那么我们将体验到每个操作员的平均奖励减少，因为每日总奖励总是受到基线的限制。换句话说，如果加入网络的人数多于基线设定的人数，则那些高于基线的额外运营商将稀释总奖励并降低每个运营商的平均奖励。因此，我们需要非常小心地设计基线函数~乙吨�~�。

评分功能

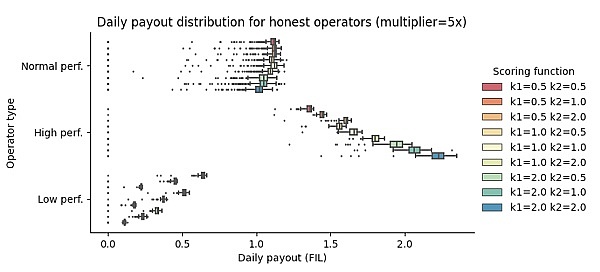
第一个观察结果是一些支出为零。这发生在运营商积累支付未来罚款所需余额的日子里。

其次，正如预期的那样，绩效对运营商的支出有重大影响，绩效高的运营商获得更高的奖励，其次是正常运营商，其次是绩效低的运营商。此外，评分函数的指数对三种运营商类型之间的支出差异有多大影响。

对于大多数指数组合，正常运营商不会对其支出产生相关影响。事实上，支出似乎主要在低绩效者和高绩效者之间流动（仅占所有运营商的 20%）。例外情况是k1=2�1=2 ，即使是普通操作员也会看到他们的奖励略有减少，以适应给予高绩效者的更高奖励。

在下图中，我们显示了每个运营商的总支出与该运营商服务的总带宽的散点图。在这里，每个点都是一个运算符，数据按评分函数和运算符类型拆分：

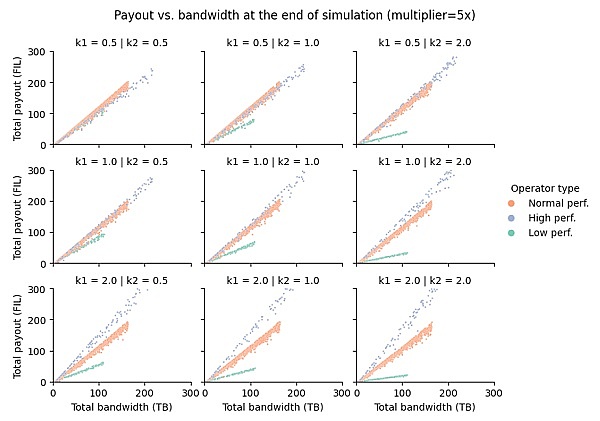
在这里，我们可以更清楚地看到各种指数对承诺带宽和奖励之间关系的影响。例如，如果我们固定（即按列查看图），我们可以看到带宽指数越小，我们对长寿的奖励就越多。这意味着，从长远来看，当较低时，在网络中停留时间更长的运营商会因贡献相同数量的带宽而获得更多回报。相反，当较高时，高性能者会因贡献相同的带宽量而获得更大的回报。现在，如果我们修复（即按行查看图），我们会观察到类似的趋势，其中增加指数k2�2k1�1k1�1k1�1k1�1k2�2导致三类运营商之间的差距越来越大。然而，效果不如增加带宽指数的影响那么可观。

惩罚倍数

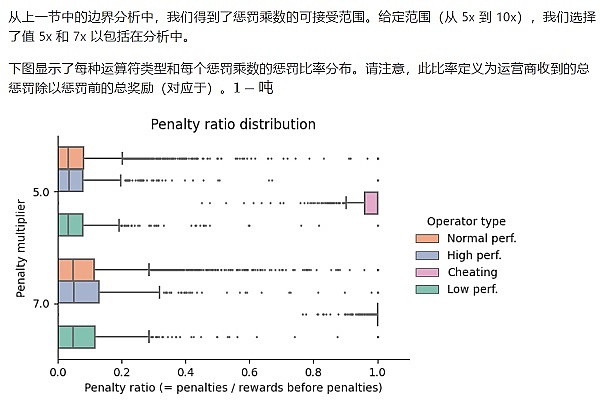
来源：金色财经